ベジエ曲線のバウンディングボックス

Bézier curve - Wikipedia, the free encyclopedia

B(t) = (1-t)^3 * P0 + 3 * (1-t)^2 * t * P1 + 3 * (1-t) * t^2 * P2 + t^3 * P3
なので
B'(t) = -3 * P0 * (1 - t)^2 + 3 * P1 * (1 - t)^2 - 6 * P1 * (1 - t) * t + 6 * P2 * (1 - t) * t - 3 * P2 * t^2 + 3 * P3 * t^2
の解t = *1(-3 P0+9 P1-9 P2+3 P3!=0)のうち0~1に収まるtの時のB(t)の値を計算して、B(0) = P0、B(1) = P3とあわせて最小値と最大値を求めればいいな。たぶん。後で実装しよう。

---

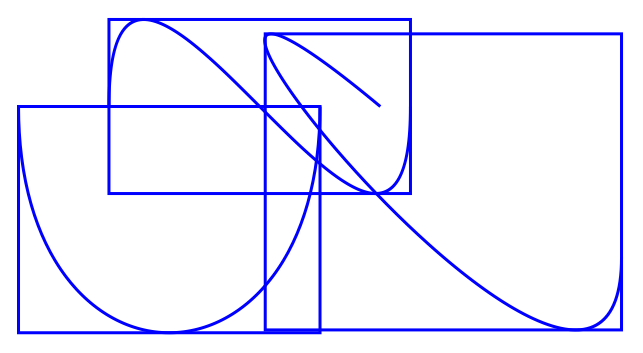
あってそう。

(ここにあったコードは全然あっていなかったので削除しました)

---

こんどこそあってそう。

---

うひひ。

5次元の空間上に分布しているので切断面を変えると色々変わる。

---

しばらく動かしてみて特に目立った問題が見つからないので公開。MIT Licenseで、とか書いておくと使いやすいのかな？？

    def calc_box(start, curves):
        P0 = start
        bounds = [[P0[0]], [P0[1]]]

        for c in curves:
            P1, P2, P3 = (
                (c[0], c[1]), 
                (c[2], c[3]), 
                (c[4], c[5]))

            bounds[0].append(P3[0])
            bounds[1].append(P3[1])

            for i in [0, 1]:
                f = lambda t: (
                    (1-t)**3 * P0[i] 
                    + 3 * (1-t)**2 * t * P1[i] 
                    + 3 * (1-t) * t**2 * P2[i]
                    + t**3 * P3[i])

                b = float(6 * P0[i] - 12 * P1[i] + 6 * P2[i])
                a = float(-3 * P0[i] + 9 * P1[i] - 9 * P2[i] + 3 * P3[i])
                c = float(3 * P1[i] - 3 * P0[i])

                if a == 0:
                    if b == 0:
                        continue
                    t = -c / b
                    if 0 < t < 1: 
                        bounds[i].append(f(t))
                    continue

                b2ac = b ** 2 - 4 * c * a
                if b2ac < 0: 
                    continue
                t1 = (-b + sqrt(b2ac))/(2 * a)
                if 0 < t1 < 1: bounds[i].append(f(t1))
                t2 = (-b - sqrt(b2ac))/(2 * a)
                if 0 < t2 < 1: bounds[i].append(f(t2))

            P0 = P3

        x = min(bounds[0])
        w = max(bounds[0]) - x
        y = min(bounds[1])
        h = max(bounds[1]) - y
        return (x, y, w, h)

*1:-6 P0+12 P1-6 P2)+-sqrt((6 P0-12 P1+6 P2)^2-4 (3 P1-3 P0) (-3 P0+9 P1-9 P2+3 P3)))/(2 (-3 P0+9 P1-9 P2+3 P3